秘書問題
数学Ⅲ既習者(難関大対策+) ★★★
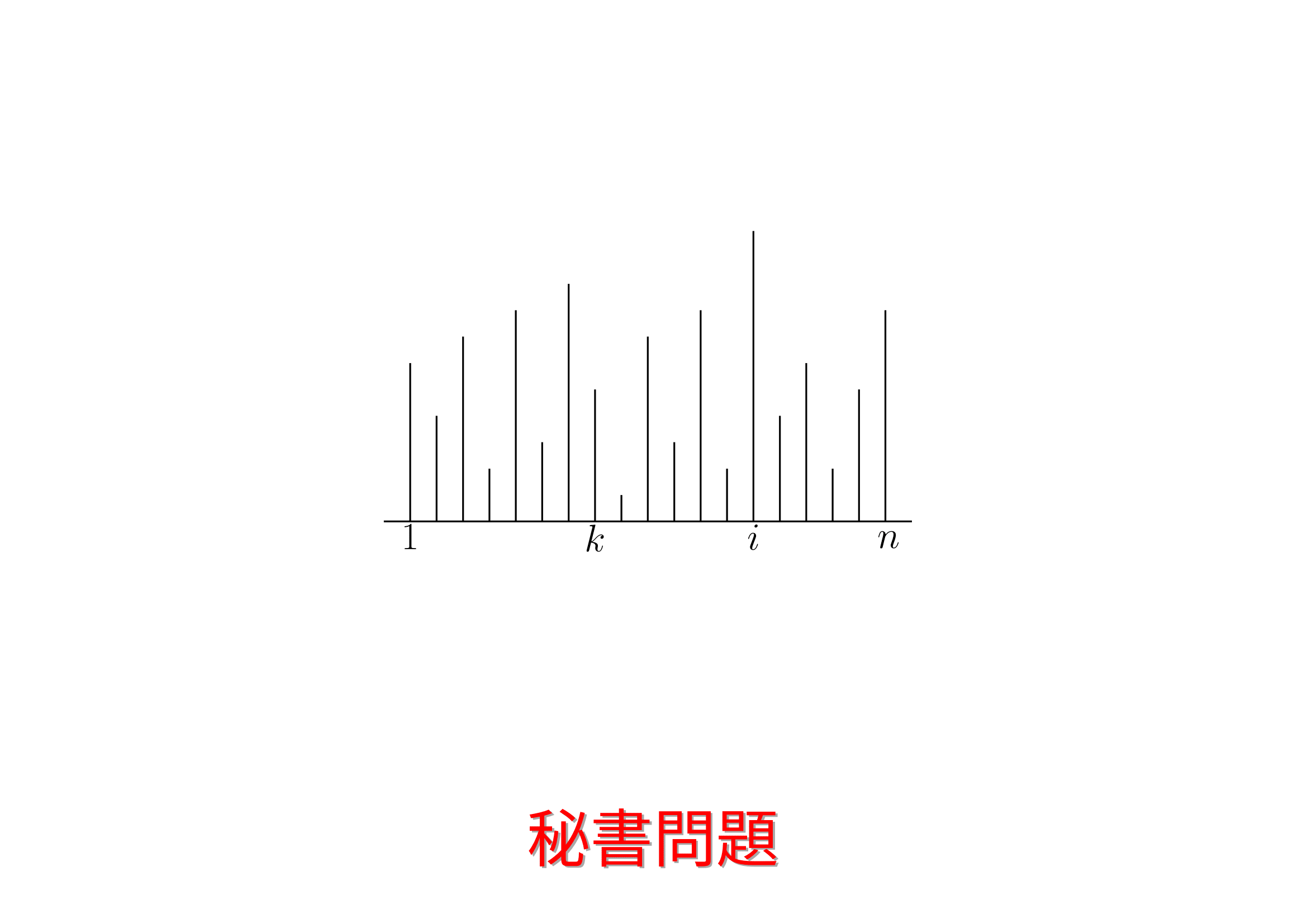
秘書問題と,大学入試における関連問題を扱います.
実用的かは意見が分かれそうですが,高校数学のネタとして面白いと思います.
秘書問題
秘書の採用担当になったつもりで考えてください(実際には秘書でなくていいのでお見合いの結婚相手等でもOKです).以下の問題を秘書問題(最適停止問題,結婚問題)と言うそうです.
秘書問題
・$n$ 人の秘書が応募をしてきて1人だけ採用する.
・$n$ 人の秘書を順番に面接し能力値(実数値)を確認する(面接しないと能力値は確認できない).面接の度に採用か不採用か決め,不採用にしたら後から採用にはできない.
・はじめの $k$ 人までは様子見する(不採用にする).この中で最大の能力をもつ秘書を越える秘書が $k+1$ 人目以降で現れたら採用する.
$n$ が十分大きいとき,$k=\dfrac{n}{e}$ のとき,最大の能力をもつ秘書を採用できる確率が最大である.
解説
$n$ を無限大に近づけたときの近似の話であることをご了承ください.

最大の能力をもつ秘書を採用できる確率を $P(k)$ とする.$i$ 番目に最大の能力をもつ秘書がいるとする.
(ⅰ) $i \leqq k$ のとき,最大の能力をもつ秘書を採用できる確率は $0$.
(ⅱ) $k+1 \leqq i \leqq n$ のとき
$i$ 番目に最大の能力をもつ秘書がいる確率は $\dfrac{1}{n}$.そして最初から $i-1$ 番目までの候補者の中で,様子見した $k$ 人の中に最大の候補者がいる確率は $\dfrac{k}{i-1}$.
以上より
$P(k)$
$\displaystyle =\sum_{i=k+1}^{n}\dfrac{1}{n}\cdot \dfrac{k}{i-1}$
$\displaystyle =\dfrac{k}{n}\sum_{i=k+1}^{n}\dfrac{1}{i-1}$
$\displaystyle =\dfrac{k}{n}\left(\dfrac{1}{k}+\dfrac{1}{k+1}+\dfrac{1}{k+2}+\cdots+\dfrac{1}{n-1}\right)$
$\displaystyle =\dfrac{k}{n}\sum_{j=k}^{n-1}\dfrac{1}{j}$
$k$ は $n$ に依存する値(この問いは $n$ と $k$ の比が問題なので),$n$ が十分大きいとき $k$ もそれに応じて大きくなるが,$n \to \infty$ において
$\displaystyle \sum_{j=k}^{n-1}\dfrac{1}{j}\fallingdotseq \sum_{j=k}^{n}\dfrac{1}{j} \to \log\dfrac{n}{k}$
となることを認めると
$\displaystyle P(k) \to \dfrac{k}{n}\log\dfrac{n}{k}=\dfrac{\log\dfrac{n}{k}}{\dfrac{n}{k}}$
と近似できる.$x=\dfrac{n}{k}$ として $f(x)=\dfrac{\log x}{x}$ のグラフを考えると(極大値,極小値の定義の練習問題(1)にこの関数があります),$x=\dfrac{n}{k}=e$ のとき,極大値かつ最大値 $\dfrac{1}{e}$ を取ることがわかります.つまり,$k=\dfrac{n}{e}$ のとき,最大の能力をもつ秘書を採用できる確率が最大.
※ 本来 $\displaystyle P(k)=\dfrac{k}{n}\sum_{j=k}^{n-1}\dfrac{1}{j}$ を数列の最大・最小の考え方で最大となる $k$ を求めるべきですが,簡潔な解を求めることが困難なようです.
※ $n \to \infty$ において $\displaystyle \sum_{j=k}^{n}\dfrac{1}{j} \to \log\dfrac{n}{k}$ となることはグラフで考察するとわかりやすいです.
具体的に $n=10$ 〜 $20$ までのときの $P(k)$ を最大にする $k$ とその最大値をChatGPTにお願いしたところ
$n=10$ → $k=3$ (約 $0.398690$ )
$n=11$ → $k=4$ (約 $0.398413$ )
$n=12$ → $k=4$ (約 $0.395515$ )
$n=13$ → $k=5$ (約 $0.392261$ )
$n=14$ → $k=5$ (約 $0.391714$ )
$n=15$ → $k=5$ (約 $0.389410$ )
$n=16$ → $k=6$ (約 $0.388086$ )
$n=17$ → $k=6$ (約 $0.387316$ )
$n=18$ → $k=6$ (約 $0.385406$ )
$n=19$ → $k=7$ (約 $0.385040$ )
$n=20$ → $k=7$ (約 $0.384209$ )
もっと $n$ を増やすと $P(k)$ はおよそ $\dfrac{1}{e} = 0.367879\cdots$ に,$\dfrac{k}{n}=\dfrac{1}{e}$ に落ち着くようです.
数Ⅲ未修者に伝えるときはだいたい $\dfrac{k}{n}=\dfrac{1}{3}$ とするとよいと言うとわかりやすいですかね.
練習問題
練習
$n$ 枚のカードの表(おもて)面に相異なる整数値が書かれている.ただし,どのような数値が書かれているのかはあらかじめわかっていない.
はじめにすべてのカードが裏返しておかれている.ここから1枚ずつ好きなカードをめくっていき,書かれている数値が $n$ 枚のカードの中で最大だと思ったらめくるのをやめるという1人ゲームを考える.$n$ 枚のカードをすべてめくり終えてしまった場合,次にめくるカードがないのでゲームは終了である.
ゲームの勝敗は,最後にめくったカードに書かれていた数値が $n$ 枚のカードの中で最大であれば勝ち,そうでなければ負けとする.
$n$ 未満の自然数 $k$ について以下の戦略 $S_k$ を考える:
はじめの $\boldsymbol{k}$ 枚までは必ずめくり,その $\boldsymbol{k}$ 枚に書かれていた数値のうち最大のものを $\boldsymbol{M}$ とする.$\boldsymbol{k+1}$ 枚目以降で $\boldsymbol{M}$ より大きな数が書かれたカードをめくったら,ただちにめくるのをやめる.
戦略 $S_k$ にしたがった場合に,このゲームに勝つ確率を $P_{n,k}$ とする.以下の問いに答えよ.
(1) $P_{3,1}$ を求めよ.
(2) $i$ を $k+1$ 以上,$n$ 以下の整数とする.戦略 $S_k$ にしたがった場合に,ちょうど $i$ 枚のカードをめくって勝つ確率を求めよ.
(3) $n$ が十分に大きいとき,戦略 $S_k$ を使ってどのくらい勝つことが出来るのかを考えてみよう.$n$ に対してどのくらいの $k$ を用いるかによって勝てる確率が変わる.簡単にするため,$n=3p$ の場合を考える.ただし,$p$ は自然数である.このとき $k=p$ として,極限値
$\displaystyle \lim_{p \to \infty} P_{n,k}$
を求めよ.
練習の解答 出典:2016横浜市立大医学部
(1)
$1,2,3$ の3枚のカードがあるとします.順列で考えて
$1,3,2$
$2,1,3$
$2,3,1$
であれば勝てるので
$P_{3,1}=\dfrac{3}{3!}=\boldsymbol{\dfrac{1}{2}}$
(2)
$i$ 番目に最大の数値がある確率は $\dfrac{1}{n}$.そして最初から $i-1$ 番目までの数値の中で,様子見した $k$ 個の中に最大の数値がある確率は $\dfrac{k}{i-1}$.求める確率は
$\dfrac{1}{n}\cdot \dfrac{k}{i-1}=\boldsymbol{\dfrac{k}{n(i-1)}}$
(3)
(2) より $\displaystyle P_{n,k}=\sum_{i=k+1}^{n}\dfrac{k}{n(i-1)}$
$n=3p$ かつ $k=p$ のとき
$\displaystyle \lim_{p \to \infty}P_{n,k}$
$\displaystyle =\lim_{p \to \infty}\sum_{i=k+1}^{n}\dfrac{p}{3p(i-1)}$
$\displaystyle =\lim_{p \to \infty}\dfrac{1}{3}\sum_{i=p+1}^{3p}\dfrac{1}{(i-1)}$
$\displaystyle =\lim_{p \to \infty}\dfrac{1}{3}\sum_{l=p}^{3p-1}\dfrac{1}{l}$
$\displaystyle =\lim_{p \to \infty}\dfrac{1}{3}\cdot \dfrac{1}{p}\sum_{l=p}^{3p-1}\dfrac{1}{\dfrac{l}{p}}$
$\displaystyle =\dfrac{1}{3}\int_{1}^{3}\dfrac{1}{x}\,dx$ ←区分求積
$\displaystyle =\boldsymbol{\dfrac{1}{3}\log 3}$
