数列の和の面積評価
積分(数学Ⅲ)(教科書範囲) ★★★
数列の和の定積分による面積評価について扱います.
数列の和の面積評価
$1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\cdots+\dfrac{1}{100^2}$
上のような 数列の和はΣ計算で求めるのが困難な和です.しかし,$y=\dfrac{1}{x^2}$ を定積分で求めることで上の和を不等式で評価できます.
図をうまく書くことが問題なので,以下に例題で解説していきます.
例題と練習問題
例題
例題
$2$ 以上の自然数 $n$ において
$\log(n+1)<1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}<1+\log n$
が成り立つことを証明せよ.
講義
まず,$y=\dfrac{1}{x}$ 上の $x=1$,$2$,$3$,$\cdots$,$n$ の点から $x$ 軸まで線分を下ろします.そして,長方形をそれぞれ右に作るか左に作るかして,図を書いて考えます.
数列の和を横の長さが $1$ の長方形の面積の和と捉えて,定積分で評価します.
解答
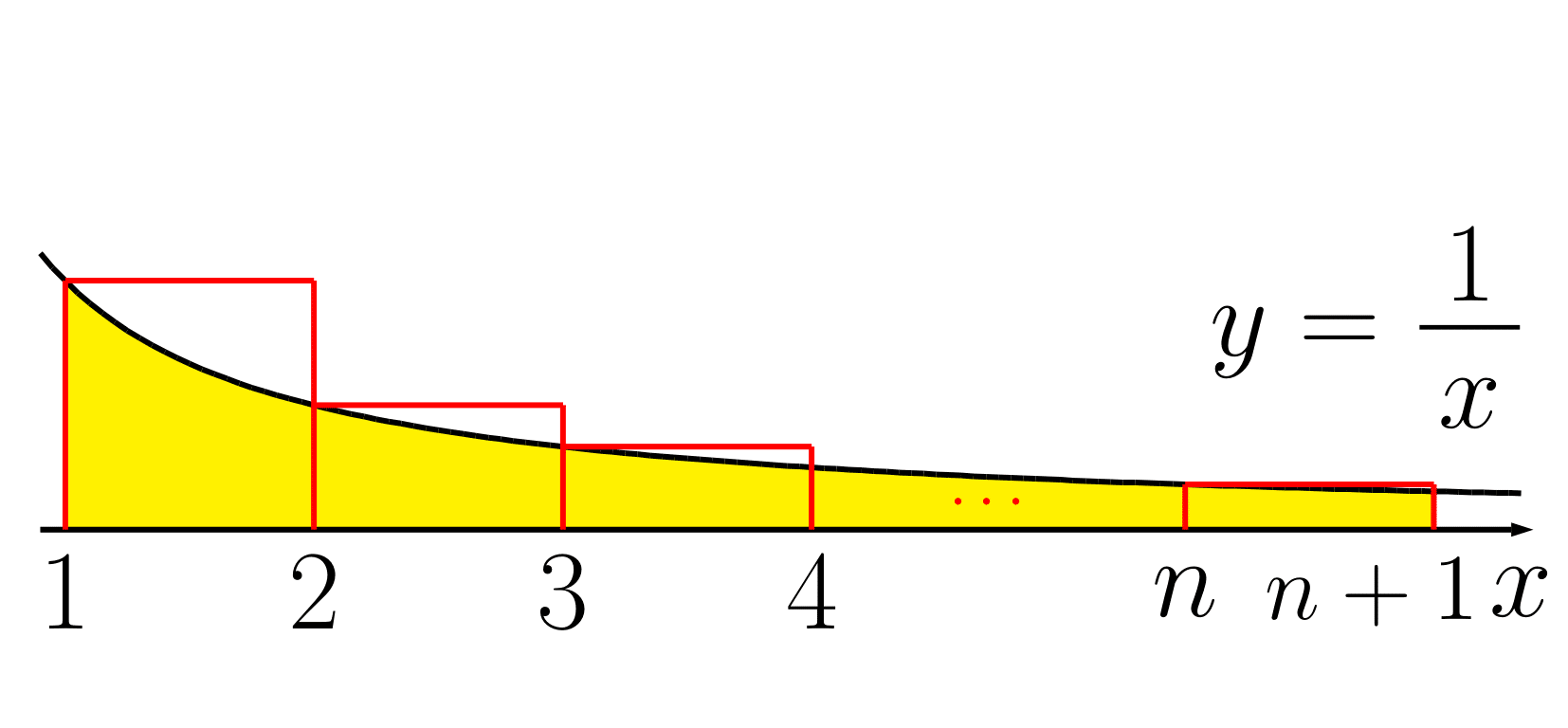
$y=\dfrac{1}{x}$ は単調減少なので,図より
$\displaystyle 1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}> \int_{1}^{n+1}\dfrac{1}{x}\,dx=\log(n+1)$

図より
$\displaystyle 1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}< 1+\int_{1}^{n}\dfrac{1}{x}\,dx=1+\log n$
$\therefore \ \log(n+1)<1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}<1+\log n$
※ $\displaystyle 1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}< \int_{0}^{n}\dfrac{1}{x}\,dx$ とすると評価が甘いですし,高校数学の範囲外の定積分(広義積分)になります.評価を厳しくする場合は $\displaystyle 1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}< 1+\dfrac{1}{2}+\int_{2}^{n}\dfrac{1}{x}\,dx$ 等のように,直接足す長方形を増やして積分範囲を狭くしていきます.
※ 無限級数に記載してありますが,$\displaystyle 1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}> \log(n+1)$ より,左辺の極限(調和級数)は発散することがわかります.項の極限は収束するのに無限級数が発散する有名な例です.
練習問題
練習
$2$ 以上の自然数 $n$ において
$\dfrac{19}{12}-\dfrac{1}{n+1}\leqq 1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\cdots+\dfrac{1}{n^2}\leqq \dfrac{7}{4}-\dfrac{1}{n}$
が成り立つことを証明せよ.
解答
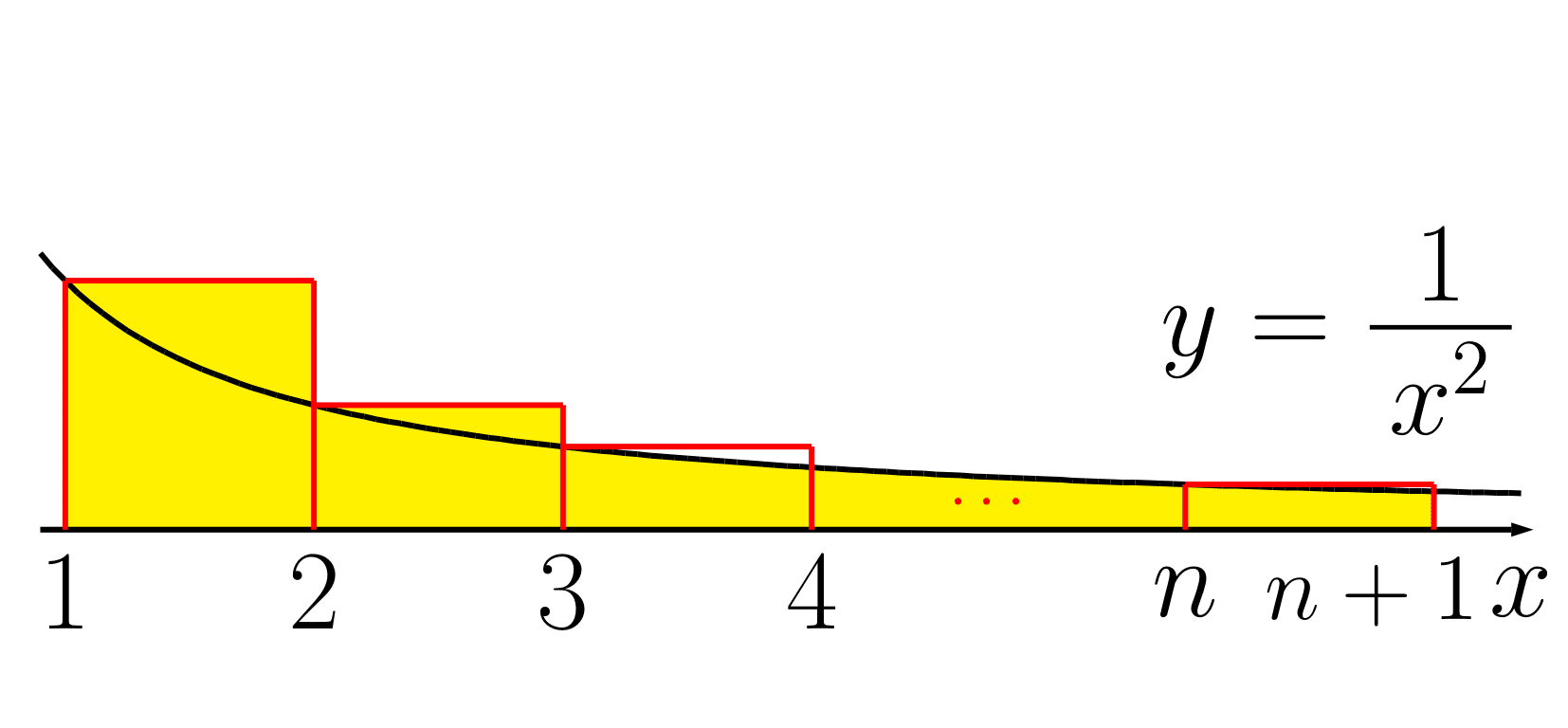
$y=\dfrac{1}{x^2}$ は単調減少なので,図より
$\displaystyle 1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\cdots+\dfrac{1}{n^2}$
$\displaystyle \geqq 1+\dfrac{1}{2^2}+\int_{3}^{n+1}\dfrac{1}{x^2}\,dx$
$=\dfrac{5}{4}+\left[-\dfrac{1}{x}\right]_{3}^{n+1}$
$=\dfrac{19}{12}-\dfrac{1}{n+1}$
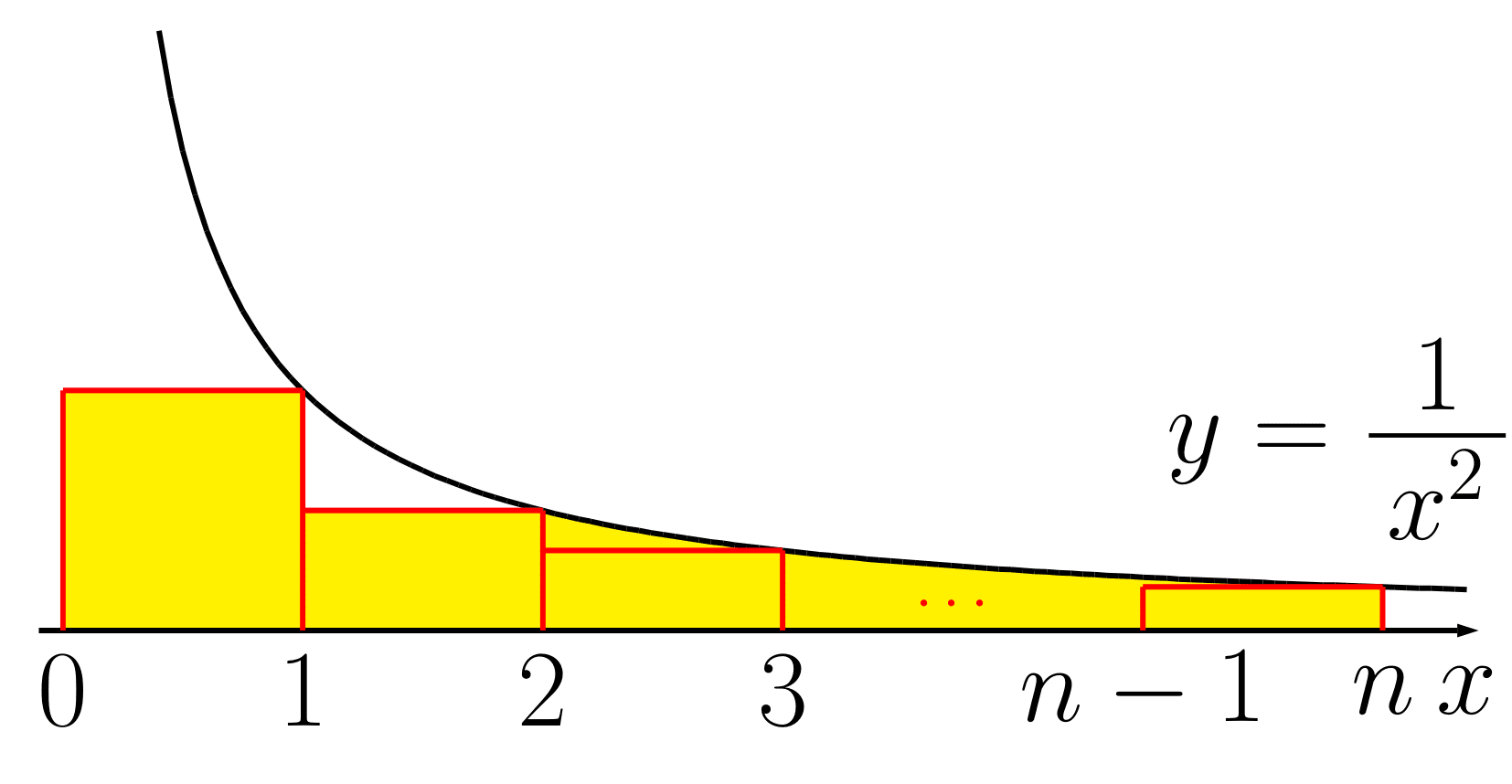
図より
$\displaystyle 1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\cdots+\dfrac{1}{n^2}$
$\displaystyle \leqq 1+\dfrac{1}{2^2}+\int_{2}^{n}\dfrac{1}{x^2}\,dx$
$=\dfrac{5}{4}+\left[-\dfrac{1}{x}\right]_{2}^{n}$
$=\dfrac{7}{4}-\dfrac{1}{n}$
※ $x$ の値が小さいと誤差が大きいので,今回は2つの長方形は直接足した評価になりました.もっと直接足す長方形を増やしていけばもっと厳しく評価できます.
※ このページ最初の問いである $1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\cdots+\dfrac{1}{100^2}$ の値は $\dfrac{19}{12}-\dfrac{1}{101}\leqq 1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\cdots+\dfrac{1}{100^2}\leqq \dfrac{7}{4}-\dfrac{1}{100}$ に収まることが示せました.ちなみに $\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{n^2}$ はバーゼル級数と呼ばれ,$\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{n^2}=\dfrac{\pi^2}{6}$ となることが知られていて,大学入試でもたまに見かけます.
