因数分解
数と式(教科書範囲) ★★★
因数分解の公式と解法を整理します.
このページは数学Ⅱの因数定理による因数分解は含めていません.
因数分解の公式
因数分解の公式
中学範囲
① $ma+mb=m(a+b)$
② $a^{2}+2ab+b^{2}=(a+b)^{2}$
③ $a^{2}-2ab+b^{2}=(a-b)^{2}$
④ $a^{2}-b^{2}=(a+b)(a-b)$
⑤ $x^{2}+(a+b)x+ab=(x+a)(x+b)$
高校範囲
⑥ $acx^{2}+(ad+bc)x+bd=(ax+b)(cx+d)$
⑦ $a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})$
⑧ $a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})$
⑨ $a^{3}+3a^{2}b+3ab^{2}+b^{3}=(a+b)^{3}$
⑩ $a^{3}-3a^{2}b+3ab^{2}-b^{3}=(a-b)^{3}$
⑪ $a^{2}+b^{2}+c^{2}+2ab+2bc+2ca=(a+b+c)^{2}$
⑫ $a^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)$
※⑦〜⑪は現行過程では厳密には数学Ⅱです.
展開公式と主な出題パターンと解き方で書いた展開公式の逆になります.
⑫ は大学入試で稀に出題されます(例題2).
因数分解の解き方
因数分解には下記のように解くためのマニュアルが存在し,どれかのパターンに落ち着くはずです.勘や閃きに頼って解くものではありません.
因数分解の解法マニュアル
どんな問題もまずⅠ,Ⅱ,Ⅲを試みます.
Ⅰ 共通因数があればくくる(全体ではなく個別にくくっても可)
Ⅱ 公式が使えるか検討する(上の公式⑥はたすきがけで対処).
Ⅲ 同じ形を別の文字で置き換える.その後,因数分解の公式が使える形まで変形.
↓
以上で最後まで解けない場合は下のいずれか,あるいは組み合わせて解きます.
・文字が1種類のとき
Ⅳ 複2次式( $\boldsymbol{ax^{4}+bx^{2}+c}$ の形)であれば強引に2乗の差を作る.
・文字が2種類以上のとき
Ⅴ 最低次数の文字について整理する.
以下の例題と練習問題で,上のマニュアルを具体的に確認していきます.
例題と練習問題
例題
例題1
次の式を因数分解せよ.
(1) $12xy^{3}-27x^{3}y$
(2) $6x^{2}+x-1$
(3) $16a^{3}+54b^{3}$
(4) $(x^{2}-2x)^{2}-11(x^{2}-2x)+24$
(5) $x(x-1)(x-2)(x-3)-24$
(6) $a^{3}-a^{2}b-ac^{2}+bc^{2}$
(7) $2x^{2}-5xy-3y^{2}+x+11y-6$
(8) $x^{4}+9x^{2}+25$
例題2 (対称式と基本対称式が既習の意欲的な人向け)
(1) $a^{3}+b^{3}$ を $a+b$ と $ab$ で表せ.
(2) $a^{3}+b^{3}+c^{3}-3abc$ を因数分解せよ.
講義
上の解法マニュアルのどのステップを踏めばいいのか※印で説明します.
例題1の解答
(1) $12xy^{3}-27x^{3}y$
$=3xy(4y^{2}-9x^{2})$
$=\boldsymbol{3xy(2y+3x)(2y-3x)}$
※ Ⅰ→Ⅱで公式④.
(2) $6x^{2}+x-1$
$=\boldsymbol{(2x+1)(3x-1)}$
※ Ⅱ.たすきがけをします(下に説明を格納しました).
たすきがけの手順
たすきがけの手順
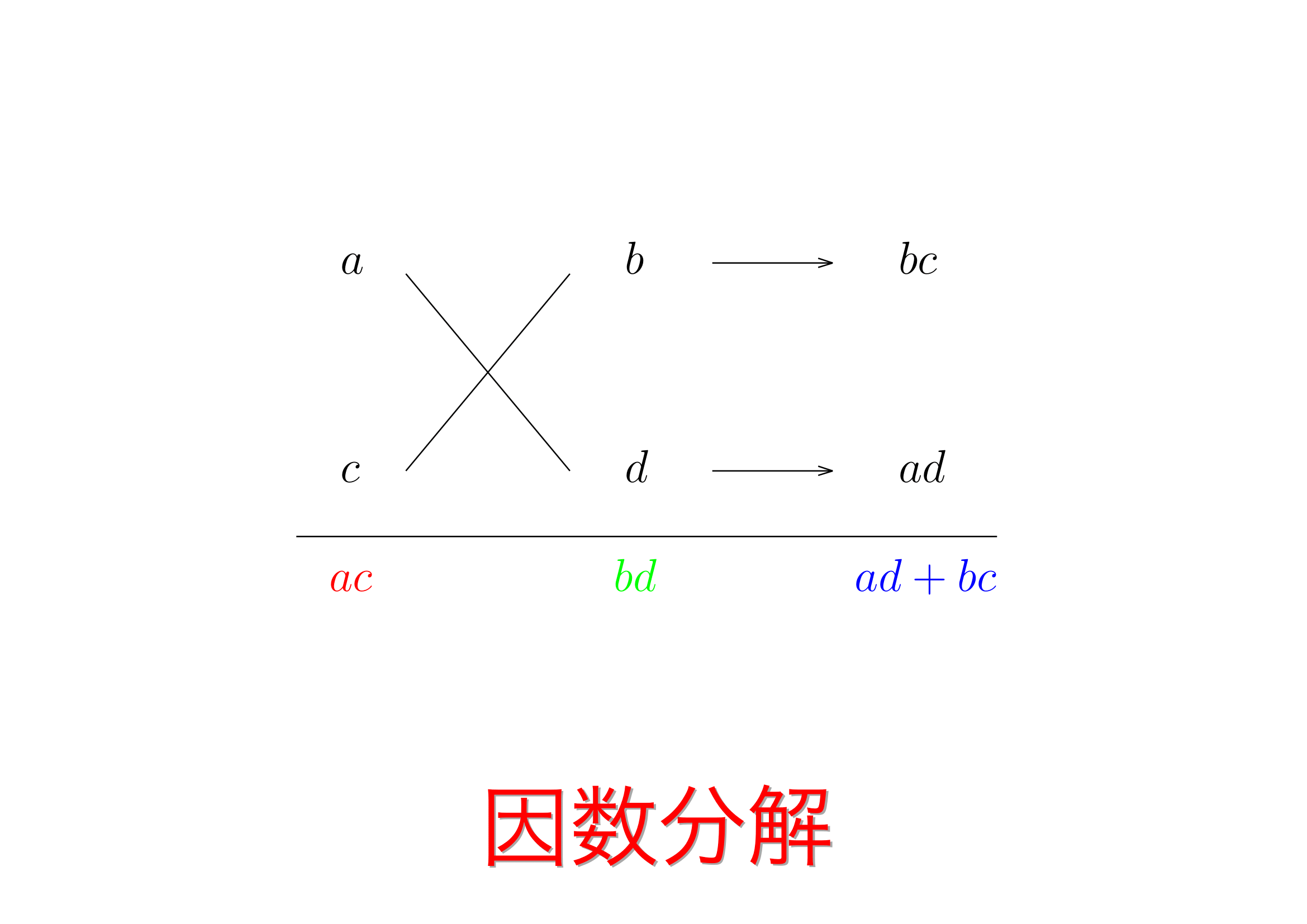
公式⑥ $\color{red}{ac}x^{2}+\color{blue}{(ad+bc)}x+\color{green}{bd}=(ax+b)(cx+d)$ で下のように $a$,$b$,$c$,$d$ を見つける手順をたすきがけ と言います.
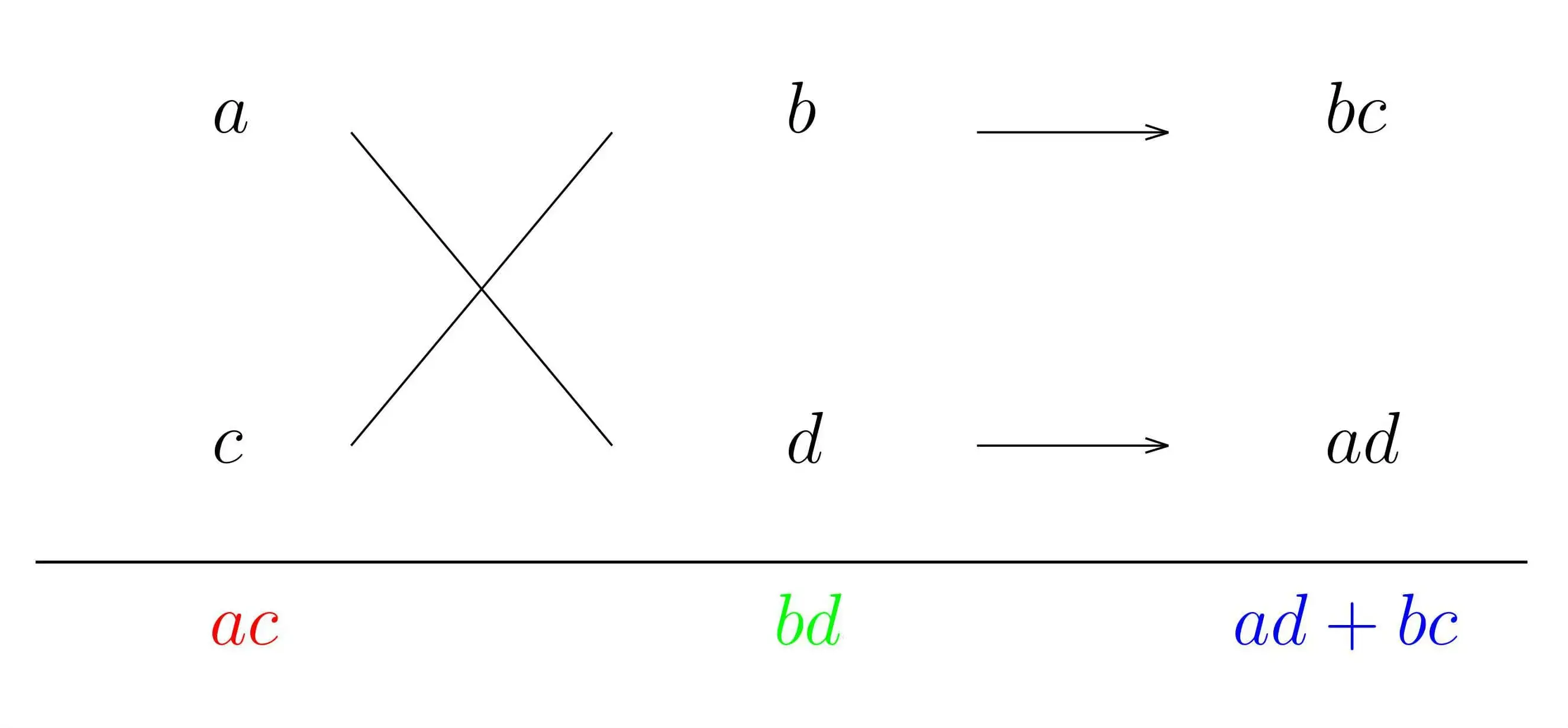
(ⅰ)まず,$\color{red}{6}x^{2}+\color{blue}{1}\cdot x+\color{green}{(-1)}$ として,$\color{red}{6(x^{2} の係数)}$,$\color{green}{-1(定数項)}$,$\color{blue}{1(x の係数)}$ の順に下のように書きます.
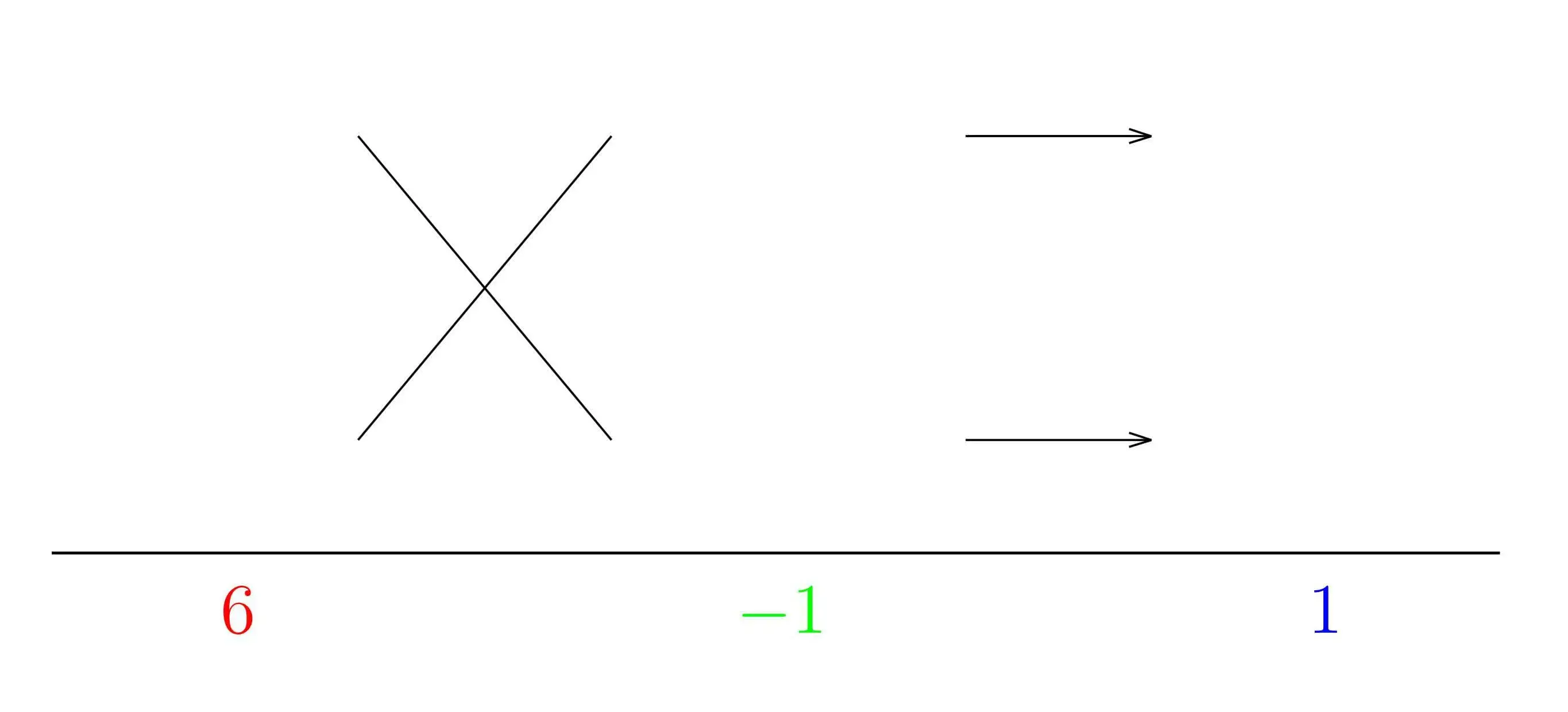
(ⅱ)次にかけて $\color{red}{6}$ になる自然数の組み合わせを考えます.今回は $2$ と $3$ を書いてみます( $1$ と $6$ だと後でうまくいきません).
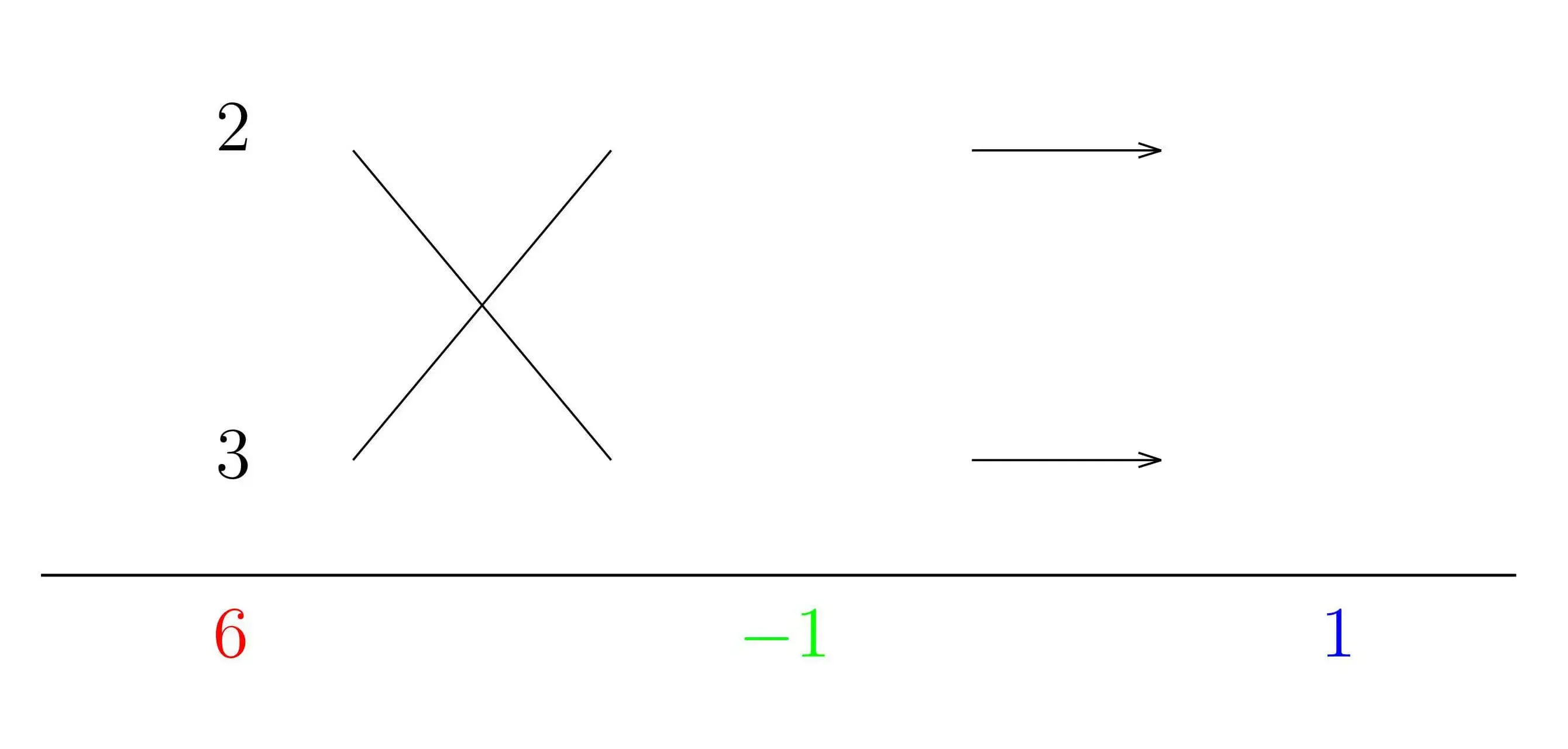
(ⅲ)クロスしてかけたものの和が $\color{blue}{1}$ になるように,かけて $\color{green}{-1}$ になる整数の組み合わせを考えます.下のようになりますね.
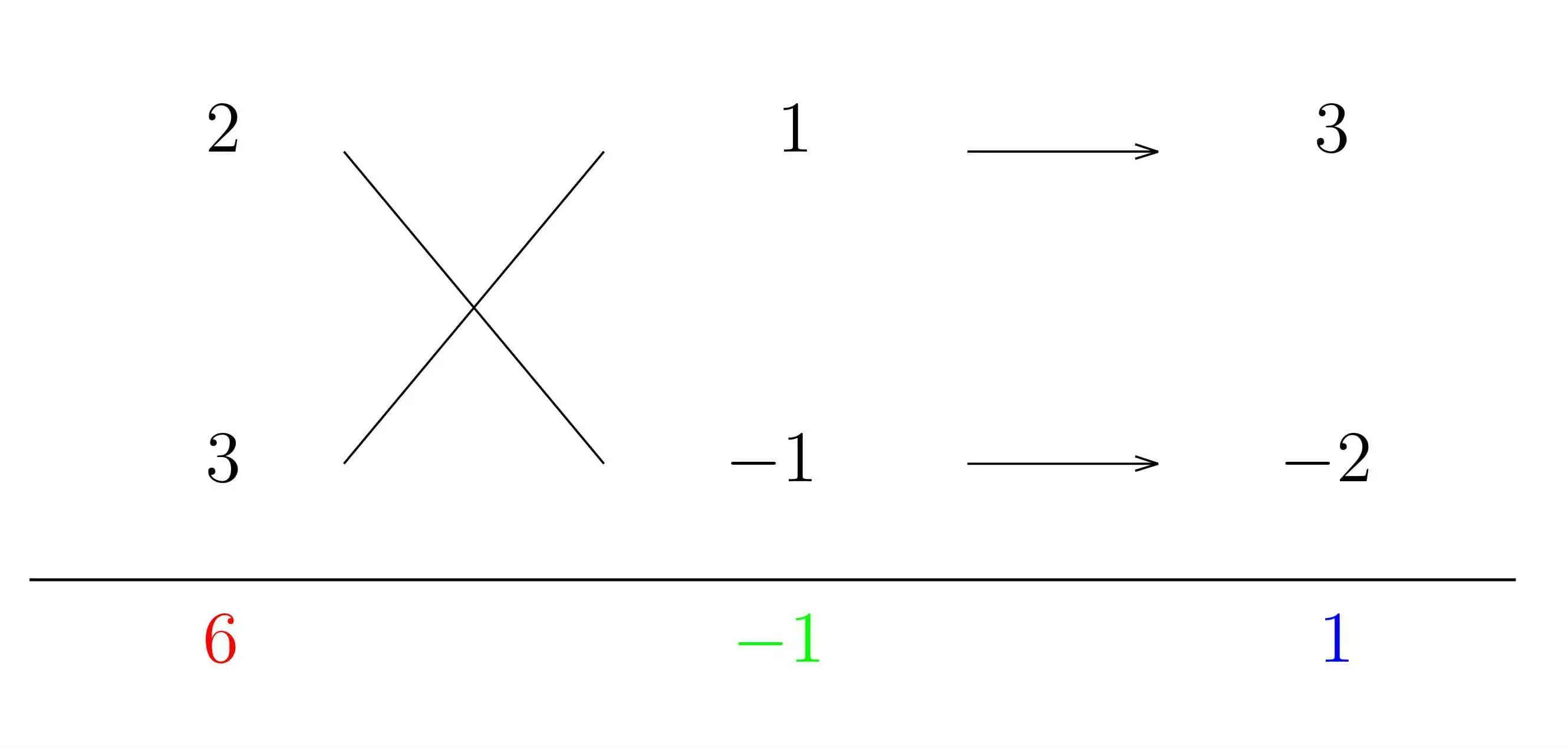
これで $a=2$,$b=1$,$c=3$,$d=-1$ より,$6x^{2}+x-1=\boldsymbol{(2x+1)(3x-1)}$ となりました.
(3) $16a^{3}+54b^{3}$
$=2(8a^{3}+27b^{3})$
$=\boldsymbol{2(2a+3b)(4a^{2}-6ab+9b^{2})}$
※Ⅰ→Ⅱで公式⑦.
(4) $x^{2}-2x=A$ とおく.
$(x^{2}-2x)^{2}-11(x^{2}-2x)+24$
$=A^{2}-11A+24$
$=(A-3)(A-8)$
$=(x^{2}-2x-3)(x^{2}-2x-8)$
$=\boldsymbol{(x-3)(x+1)(x-4)(x+2)}$
※ Ⅲ→公式⑤.慣れると置き換えるのは面倒なので,これ以降は置き換えずに解きますね.
(5) $x(x-1)(x-2)(x-3)-24$
$=x(x-3)(x-1)(x-2)-24$
$=(x^{2}-3x)\{(x^{2}-3x)+2\}-24$
$=(x^{2}-3x)^{2}+2(x^{2}-3x)-24$
$=\{(x^{2}-3x)+6\}\{(x^{2}-3x)-4\}$
$=\boldsymbol{(x^{2}-3x+6)(x-4)(x+1)}$
※ 同じ形 $(x^{2}-3x)$ を見つけるように変形してⅢ→公式⑤.
(6) $a$ は $3$ 次,$b$ は $1$ 次,$c$ は $2$ 次なので,$b$ の $1$ 次式
$b+$
とみて整理します.
$a^{3}-a^{2}b-ac^{2}+bc^{2}$
$=\color{red}{(c^{2}-a^{2})b+a(a^{2}-c^{2})}$
$=(c^{2}-a^{2})b-a(c^{2}-a^{2})$
$=(c^{2}-a^{2})(b-a)$
$=\boldsymbol{(c+a)(c-a)(b-a)}$
※ Ⅴ→共通因数でくくって公式④.
(7) $x$,$y$ ともに $2$ 次なので,どちらで整理してもいいですが,$x$ の $2$ 次式
$x^{2}+$ $x+$
とみて整理するといいと思います.
$2x^{2}-5xy-3y^{2}+x+11y-6$
$=\color{red}{2x^{2}+(1-5y)x-3y^{2}+11y-6}$
$=2x^{2}+(1-5y)x-(3y^{2}-11y+6) \ \cdots$ ☆
$=2x^{2}+(1-5y)x-(3y-2)(y-3) \ \cdots$ ♪
$=\{2x+(y-3)\}\{x-(3y-2)\}$
$=\boldsymbol{(2x+y-3)(x-3y+2)}$
※ Ⅴ→☆で最後のカッコをたすきがけ→♪で全体をたすきがけです(下に詳しく説明しました).
♪でのたすきがけ
♪でのたすきがけの手順
(ⅰ)まず,$\color{red}{2}x^{2}+\color{blue}{(1-5y)}x+\color{green}{\{-(3y-2)(y-3)\}}$ として,$\color{red}{2(x^{2} の係数)}$,$\color{green}{-(3y-2)(y-3)(定数項)}$,$\color{blue}{1-5y(x の係数)}$ の順に下のように書きます.
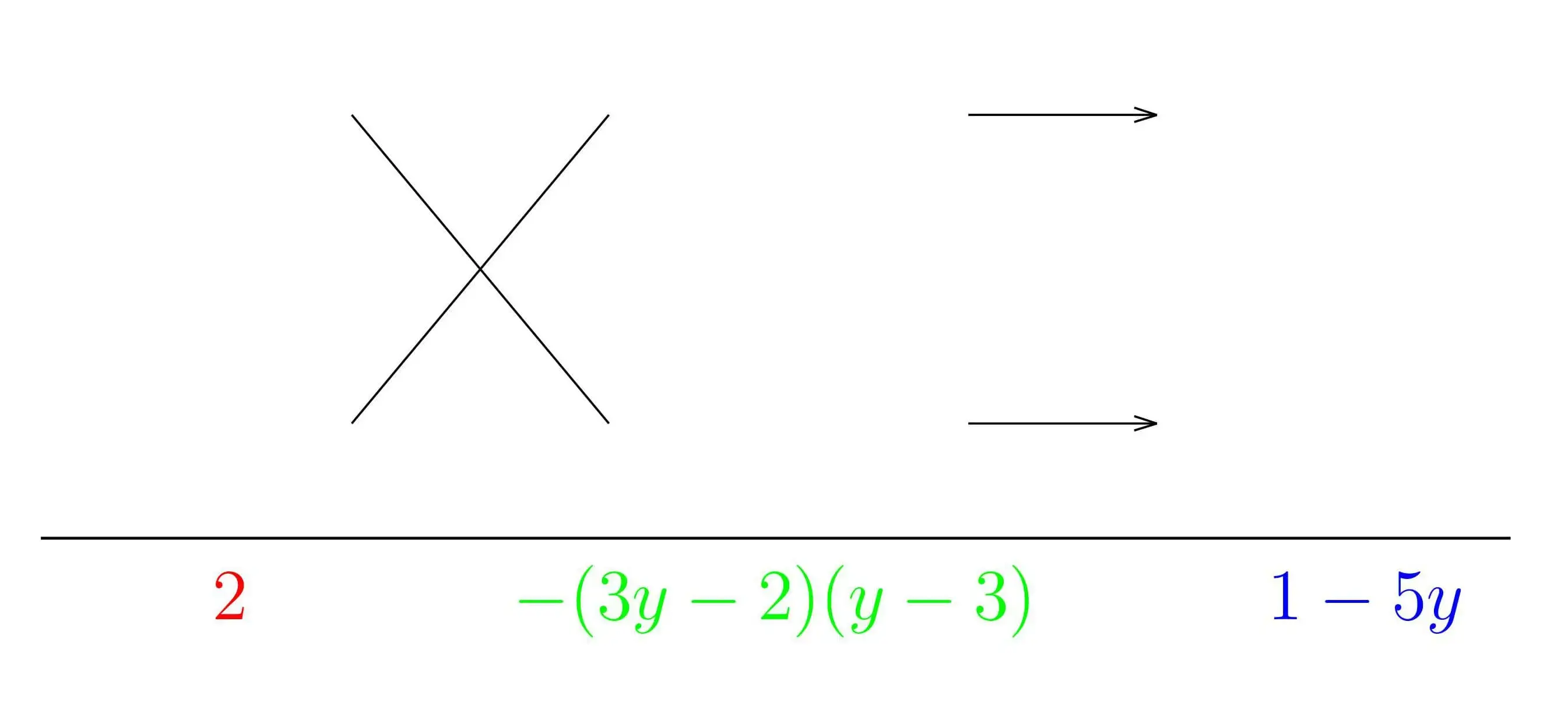
(ⅱ)次にかけて $\color{red}{2}$ になる自然数の組み合わせを考えます.今回は $2$ と $1$ で一択ですね(どちらが上でも構いません)
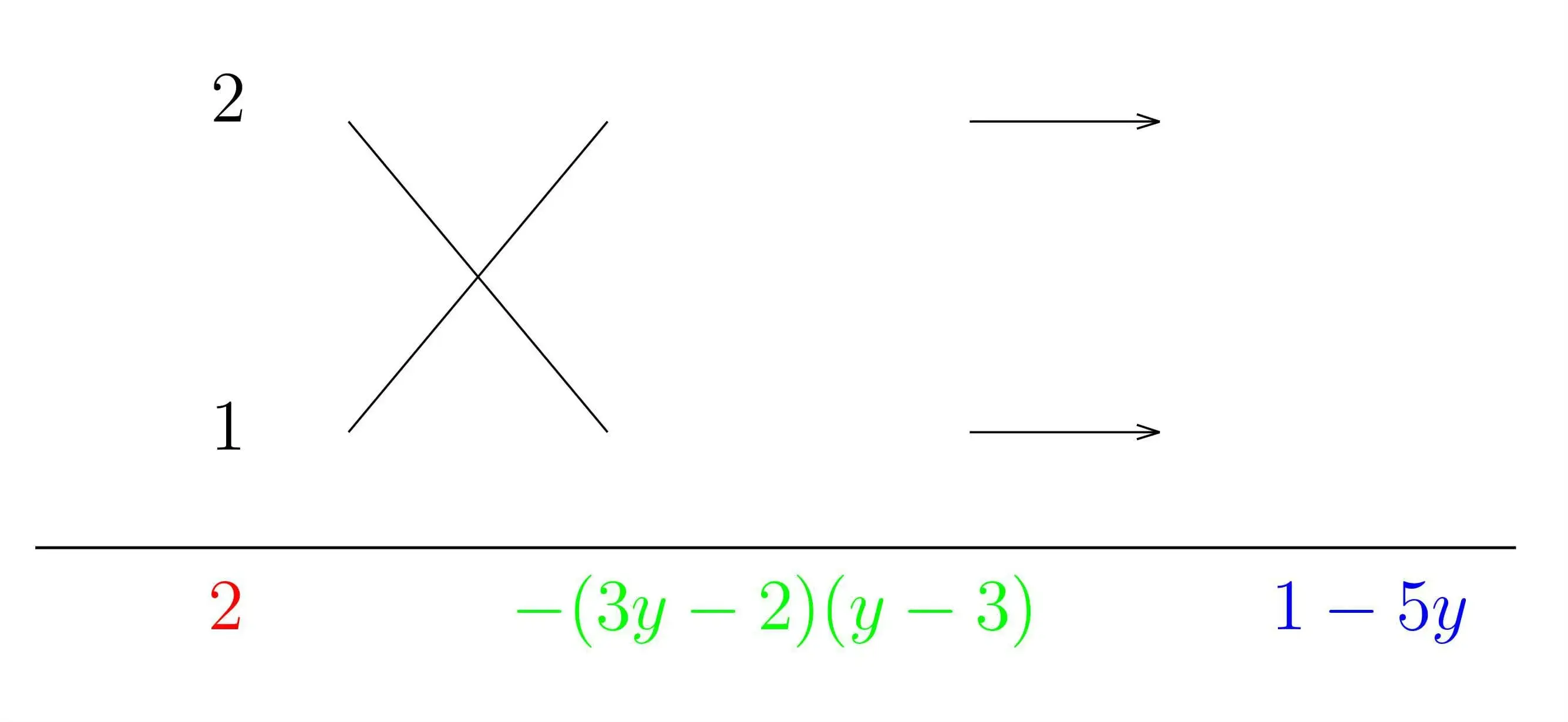
(ⅲ)クロスしてかけたものの和が $\color{blue}{1-5y}$ になるように,かけて $\color{green}{-(3y-2)(y-3)}$ になる組み合わせを考えます.下のようになりますね.
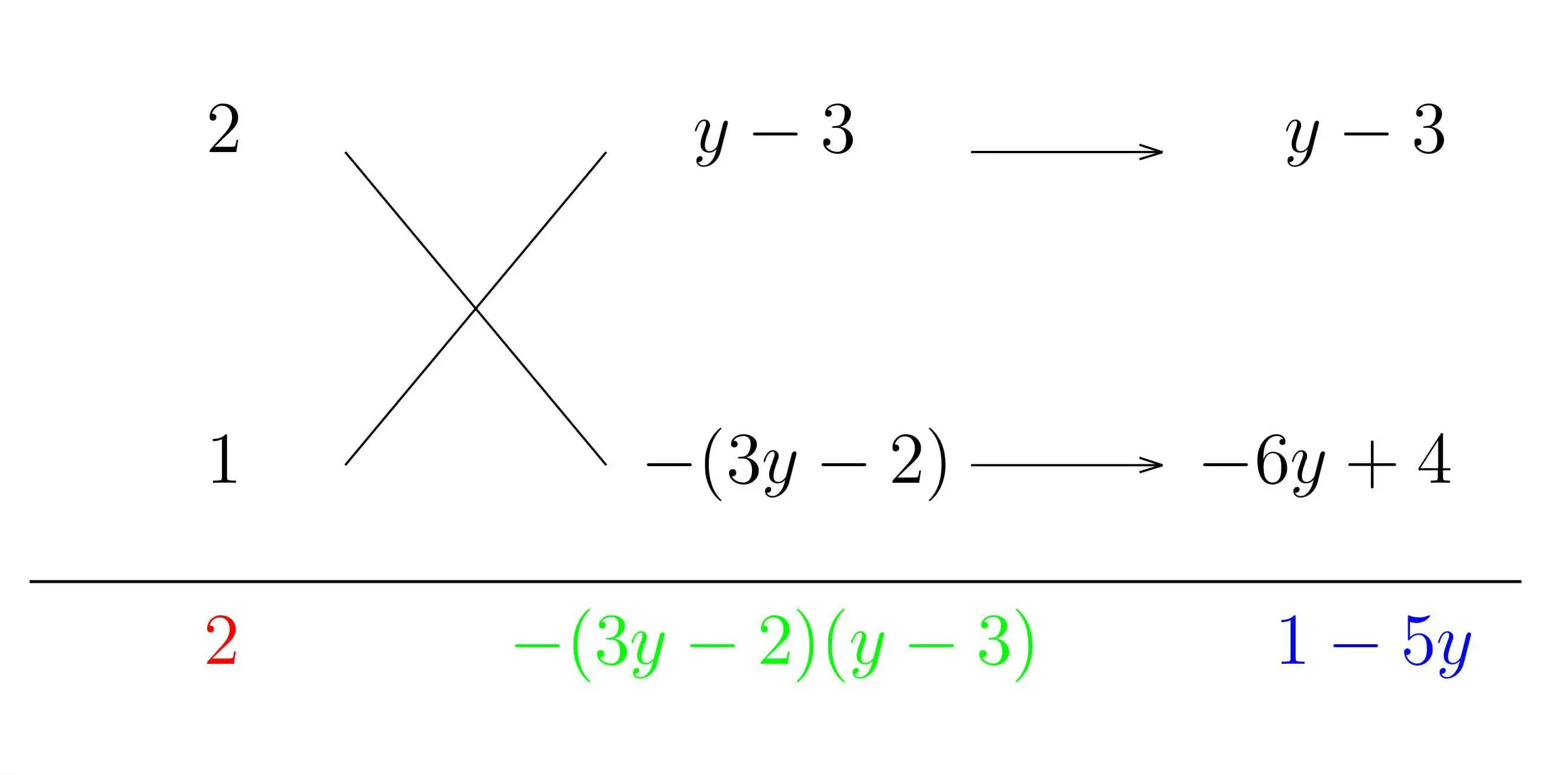
これで $2x^{2}+(1-5y)x-(3y-2)(y-3)=\{2x+(y-3)\}\{x-(3y-2)\}$ となります.
(8) $x^{4}+9x^{2}+25$
$=x^{4}+10x^{2}+25-x^{2}$
$=(x^{2}+5)^{2}-x^{2}$
$=(x^{2}+5+x)(x^{2}+5-x)$
$=\boldsymbol{(x^{2}+x+5)(x^{2}-x+5)}$
※ Ⅳです.複2次式の問題は強引に2乗 $-$ 2乗の形に持っていきます.
例題2
(1) 対称式は基本対称式で表せます.
$a^{3}+b^{3}$
$=\boldsymbol{(a+b)^{3}-3ab(a+b)}$
(2) (1)の式を使います.
$a^{3}+b^{3}+c^{3}-3abc$
$=(a+b)^{3}-3ab(a+b)+c^{3}-3abc$
$=(a+b)^{3}+c^{3}-3ab(a+b)-3abc$
$=\{(a+b)+c\}\{(a+b)^{2}-(a+b)c+c^{2}\}-3ab(a+b+c)$
$=\boldsymbol{(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)}$
練習問題
練習
次の式を因数分解せよ.
(1) $2x^{4}-5x^{2}-12$
(2) $(x^{2}+x-1)(x^{2}+x-5)+3$
(3) $(x+1)(x-2)(x+3)(x-4)+24$
(4) $8x^{3}z-24x^{3}-y^{3}z+3y^{3}$
(5) $2x^{2}-5x+5y^{2}+2y+11xy-3$
(6) $(a+b)(b+c)(c+a)+abc$
(7) $4x^{4}-16x^{2}+9$
(8) $p^{3}-q^{3}-27r^{3}-9pqr$ (例題2に対応)
(9) $(y-z)x^{3}+(z-x)y^{3}+(x-y)z^{3}$
練習の解答
(1) $2x^{4}-5x^{2}-12$
$=(2x^{2}+3)(x^{2}-4)$
$=\boldsymbol{(2x^{2}+3)(x+2)(x-2)}$
(2) $(x^{2}+x-1)(x^{2}+x-5)+3$
$=(x^{2}+x)^{2}-6(x^{2}+x)+8$
$=(x^{2}+x-4)(x^{2}+x-2)$
$=\boldsymbol{(x^{2}+x-4)(x+2)(x-1)}$
(3) $(x+1)(x-2)(x+3)(x-4)+24$
$=(x^{2}-x-2)(x^{2}-x-12)+24$
$=(x^{2}-x)^{2}-14(x^{2}-x)+48$
$=(x^{2}-x-6)(x^{2}-x-8)$
$=\boldsymbol{(x-3)(x+2)(x^{2}-x-8)}$
(4) $8x^{3}z-24x^{3}-y^{3}z+3y^{3}$
$=(8x^{3}-y^{3})z-3(8x^{3}-y^{3})$
$=\boldsymbol{(z-3)(2x-y)(4x^{2}+2xy+y^{2})}$
(5) $2x^{2}-5x+5y^{2}+2y+11xy-3$
$=2x^{2}+(11y-5)x+(5y^{2}+2y-3)$
$=2x^{2}+(11y-5)x+(5y-3)(y+1)$
$=\boldsymbol{(2x+y+1)(x+5y-3)}$
(6) $(a+b)(b+c)(c+a)+abc$
$=(b+c)\{a^{2}+(b+c)a+bc\}+bca$
$=(b+c)a^{2}+(b^{2}+2bc+c^{2}+bc)a+(b+c)bc$
$=(b+c)a^{2}+(b^{2}+3bc+c^{2})a+(b+c)bc$
$=\{a+(b+c)\}\{(b+c)a+bc\}$
$=\boldsymbol{(a+b+c)(ab+bc+ca)}$
(7) $4x^{4}-16x^{2}+9$
$=(2x^{2}-3)^{2}-4x^{2}$
$=(2x^{2}-3+2x)(2x^{2}-3-2x)$
$=\boldsymbol{(2x^{2}+2x-3)(2x^{2}-2x-3)}$
(8) 出典:2015旭川医科大
$p^{3}-q^{3}-27r^{3}-9pqr$
$=(p-q)^{3}+3pq(p-q)-27r^{3}-9pqr$
$=(p-q)^{3}-27r^{3}+3pq(p-q)-9pqr$
$=\{(p-q)-3r\}\{(p-q)^{2}+(p-q)3r+9r^{2}\}+3pq(p-q-3r)$
$=\boldsymbol{(p-q-3r)(p^{2}+q^{2}+9r^{2}+pq-3qr+3rp)}$
※公式⑫で $a=p$,$b=-q$,$c=-3r$ としても可.
(9) $(y-z)x^{3}+(z-x)y^{3}+(x-y)z^{3}$
$=(y-z)x^{3}-(y^{3}-z^{3})x+yz(y^{2}-z^{2})$
$=(y-z)\{x^{3}-(y^{2}+yz+z^{2})x+yz(y+z)\}$
$=(y-z)\{(z-x)y^{2}+(z^{2}-zx)y+x^{3}-z^{2}x\}$
$=(y-z)(z-x)\{y^{2}+zy-x(x+z)\}$
$=(y-z)(z-x)\{y+(x+z)\}(y-x)$
$=\boldsymbol{-(x-y)(y-z)(z-x)(x+y+z)}$
